comprimento. Um bloco de massa m está em repouso sobre uma superfície horizontal sem atrito. O pêndulo é largado do repouso a um ângulo de 53º com a vertical. A bola do pêndulo colide elasticamente com o bloco no ponto mais baixo de seu arco de trajetória. Após a colisão, o ângulo máximo que o pêndulo forma com a vertical é 5,73º. Determine a massa m.
 |
| Inicialmente antes de ser largado |
 |
| Sistema após a colisão. |
Para resolver este problema é preciso primeiramente saber a velocidade que o pêndulo chega até a massa m.
Devemos lembrar que a energia mecânica deve ser conservada, então a energia potencial gravitacional do pêndulo quando na posição inicial deve ser igual à energia cinética ao alcançar o bloco.
Devemos lembrar que a energia mecânica deve ser conservada, então a energia potencial gravitacional do pêndulo quando na posição inicial deve ser igual à energia cinética ao alcançar o bloco.
Assim a altura será dada por
Então a velocidade do pêndulo ao chegar ao bloco (antes da colisão) será de
Utilizamos o mesmo artifício para calcular a velocidade do bloco após a colisão, já que sabemos a altura que o bloco alcança igualamos a energia cinética do pêndulo após a colisão igualada a energia potencial gravitacional na altura menor.
Após obtermos os valores das velocidades para o pêndulo está na hora de utilizarmos dados referentes ao bloco.
Devemos observar dois fatos:
Primeiro: Como é uma colisão elástica a energia total durante a colisão também deve ser conservada.
Segundo: O momentum linear deve ser conservado.
Equacionando estes dois fatos:
M é a massa do bloco;
m é a massa do pêndulo;
v é a velocidade do bloco;
V é a velocidade do pêndulo;
O subíndice zero significa antes da colisão;
O subíndice 1 significa após a colisão.
Substituindo os valores:
Substituindo
Assim concluindo que a massa do bloco é aproximadamente 0,32 kg.
Se você gostou da resolução entre no apoia.se
https://apoia.se/10213499416137348
https://apoia.se/10213499416137348
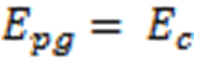
Nenhum comentário:
Postar um comentário