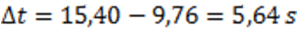PUC - MG

Um atirador dispara horizontalmente um rifle, a 40 m do alvo. Sabendo-se que a bala sai do cano com uma velocidade de 800 m/s, o desvio vertical apresentado no alvo, devido ao efeito gravitacional, em cm, é igual a:
(g = 10 m/s²)
a) 0,250
b) 0,815
c) 1,25
d) 1,85
e) 2,45

Separamos as equações nas direções verticais e horizontais.

Para a horizontal e podemos calcular o tempo que a bala chega no alvo.

x = x0 + vx.t

40 = 0 + 800.t

t= 40/800=0,05 s

Para a vertical podemos calcular a altura que ele chega:

y = y0 +v0y.t + g.t²/2

y = 0 +0.0,05+ 10 . 0,05²/2=0,0125 m = 1,25 cm

(C)

Facebook - Halliday

Um canhão antitanque acha-se localizado à beira de um platô, a uma altura de 60 m acima de uma planície que o circunda. O artilheiro vê um tanque inimigo estacionado na planície, a uma distância horizontal de 2,2 km contada a partir do canhão. No mesmo instante, a tripulação do tanque vê o canhão e começa a se afastar com uma aceleração de 0,90 m/s². Se o canhão antitanque disparar um projétil com velocidade de saída de 240 m/s, com um ângulo de elevação de 10° acima da horizontal, quanto tempo o artilheiro deverá esperar antes de fazer o disparo para que o projétil atinja o tanque?

   Primeiramente deve-se calcular o tempo que o projétil leva para tocar o solo e o local que o projétil vai aterrissar. Então usamos as equações cinemáticas para o projétil em cada uma das direções.

    Assim, o projétil chega ao chão em 9,76 s e na posição 2306,77 m.

    Sabendo isso deve-se saber quanto tempo o tanque leva para chegar a posição de chegada do projétil.

    Assim para o tanque canhão:

Resolvendo a equação:

Assim o projétil deve ser lançado 5,6 s após a partida do canhão.

UFRGS - 2014 - Questão 07

07. Uma bomba é arremessada, seguindo uma trajetória parabólica, conforme representado na figura abaixo. Na posição mais alta da trajetória, a bomba explode.

   Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem. 

   A explosão da bomba é um evento que .............. a energia cinética do sistema. A trajetória do centro de massa do sistema constituído pelos fragmentos da bomba segue .......... .

(A) não conserva - verticalmente para o solo

(B) não conserva - a trajetória do fragmento mais massivo que o da bomba

(C) não conserva - a mesma parábola anterior à explosão

(D) conserva - a mesma parábola anterior à explosão

(E) conserva - verticalmente para o solo

   Para que a bomba possa explodir é adicionado uma certa quantidade de energia tirada de reações químicas internas, assim a energia cinética é aumentada o que significa que a energia cinética do sistema não é conservada.
   O momentum linear do sistema é conservado, o que significa que o centro de massa do sistema segue linearmente sua trajetória anterior, que é uma parábola.

Resposta: item (C)